무선통신 알고리즘 1 - STBC

무선통신 알고리즘 1 - STBC (Space Time Block Coding)

STBC 가 뭐냐?

킹갓 chat GPT의 대답

→ STBC는 Space-Time Block Coding의 약자로, 공간-시간 블록 부호화를 의미.

STBC는 다중 안테나 시스템에서 전송 신호를 부호화하는 기술로, 안테나 간의 공간 및 시간 다이버시티를 활용하여 통신 신호의 안정성과 대역폭 이용률을 향상시킨다.

STBC는 다중 안테나 시스템에서 데이터를 전송할 때, 두 개 이상의 안테나를 사용하여 전송 신호를 인코딩합니다. 이 때, STBC는 여러 개의 안테나에서 전송된 신호를 일종의 블록 형태로 인코딩하여 전송하며, 수신 측에서는 블록 형태의 신호를 디코딩하여 원래의 신호를 복구한다.

이러한 STBC 기술은 무선통신 분야에서 많이 활용되며, LTE나 Wi-Fi 등 다양한 무선통신 기술에서 적용되고 있다.

STBC는 Alamouti가 1998년에 발표한 논문 ‘A simple transmit diversity technique for wireless communications’에서 처음 발표되었으며, 현대 무선통신의 근간이 되는 기술이다.

발표된 지 25년이 지났는데 아직도 사용될까?

→ 그렇다!!!!!!! STBC는 여전히 LTE와 같은 네트워크 기술에 사용되는 MIMO 기법이다. 뿐만 아니라 Wi-Fi (IEEE 802.11)이나 IEEE 802.11n, IEEE 802.11ac와 같은 Wi-Fi 표준에서도 STBC를 사용하고 있다. 앞으로도 무선통신 분야에서 계속 사용될 것으로 보인다.

어떻게 구성되는지 자세히 알아보자

먼저 송신 안테나가 2개, 수신 안테나가 1개인 무선통신 환경을 가정해본다. 송신 안테나 개수가 여러개, 수신 안테나 개수가 한 개 이므로 이를 MISO (Multiple Input Single Output) system이라고 부른다. (MIMO system으로 칭해도 문제는 없다.) 이를 도식화하면 다음과 같이 나타낼 수 있다.

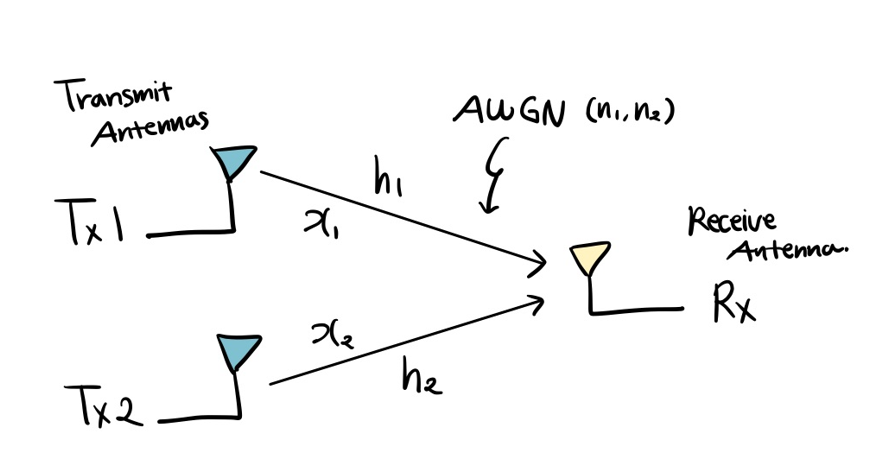
이때 수신 안테나가 두 개의 송신 안테나로 부터 받은 신호 $y_1$, $y_2$는 다음과 같이 표현된다.

\[\begin{align} y_1 = x_1h_1+n_1 \\ y_2 = x_2h_2+n_2 \end{align}\]

여기서 $x_1$과 $x_2$는 송신 안테나 Tx1, Tx2에서 각각 전송한 신호이며, $h_1$과 $h_2$는 레일리 페이딩이다. 또한, $n_1$과 $n_2$는 AWGN (Additive white gaussian noise)를 의미한다.

위와 같은 경우는 어떠한 encoding이 사용되지 않았으므로 두 개의 SISO system이라고 볼 수 있다. 즉, 안테나는 여러개를 사용했지만 시공간 diversity를 전혀 사용하지 않았다.

Alamouti는 이처럼 여러 개의 안테나를 사용하는 경우 시공간 이득을 취하는 방법인 STBC를 제안하였으며, STBC encoding matrix는 다음과 같다

\[\begin{align} X = \begin{bmatrix} x_1 & x_2 \\ -x_2^* & x_1^* \end{bmatrix} \end{align}\]

여기서, 행은 time slot의 index를 의미하며, 열은 하나의 Tx에서 두 time slot동안 전송한 데이터라고 볼 수 있다. 예를 들어 Tx1에서는 첫 번째 time에 $x_1$을 전송하며, 두 번째 time에 $-x_2^*$을 전송할 것이다.

그리고, STBC encoding matrix는 Orthogonal matrix이며 아래와 같이 간단하게 확인할 수 있다.

\[XX^H = \begin{bmatrix} x_1 & x_2 \\ -x_2^* & x_1^* \end{bmatrix} \begin{bmatrix} x_1^* & -x_2 \\ x_2^* & x_1 \end{bmatrix} = \begin{bmatrix} |x_1|^2+|x_2|^2 & 0 \\ 0 & |x_1|^2+|x_2|^2 \end{bmatrix}\]

위 STBC encoding matrix를 전송하는 경우 수신신호는 다음과 같이 표현할 수 있다.

\[\begin{bmatrix} y_1 \\ y_2 \end{bmatrix} = \begin{bmatrix} x_1 & x_2 \\ -x_2^* & x_1^* \end{bmatrix} \begin{bmatrix} h_1 \\ h_2 \end{bmatrix} +\begin{bmatrix} n_1 \\ n_2 \end{bmatrix} =\begin{bmatrix} x_1h_1+x_2h_2+n_1 \\ -x_2^*h_1+x_1^*h_2+n_2 \end{bmatrix}\]

왼쪽 수식과 오른쪽 수식은 수학적으로 동일하지만, 수신단에서는 $x$와 $h$에 대한 어떠한 정보도 없는 상태이므로 왼쪽 수식의 형태로 메시지를 분리할 수 없다. 따라서, 행렬이 전개된 형태인 오른쪽 수식을 수신한다고 판단하는 것이 옳다.

다음으로, 위 수신신호를 받은 Rx는 Decoding을 수행한다. 먼저, 수신신호를 다음과 같이 바꿔쓸 수 있다.

\[\begin{bmatrix} y_1 \\ y_2^* \end{bmatrix} = \begin{bmatrix} h_1 & h_2 \\ h_2^* & -h_1^* \end{bmatrix} \begin{bmatrix} x_1 \\ x_2 \end{bmatrix} +\begin{bmatrix} n_1 \\ n_2^* \end{bmatrix} =Hx+n\]

$y_2$에 conjugate를 취하면 위와 같이 channel matrix $H$가 information vector 앞에 곱해지는 형태로 식을 변환할 수 있다. 또한, 우리의 목표는 전송신호 $x_1$과 $x_2$를 복원하는 것이므로 수신신호 $y_2$에 취해진 conjugate 전혀 문제가 되지 않는다.

바로 위 식의 양 변에 $H^H$를 곱한다.

\[\begin{align} H^H\begin{bmatrix} y_1 \\ y_2^* \end{bmatrix} =\begin{bmatrix} h_1^* & h_2 \\ h_2^* & -h_1 \end{bmatrix}\begin{bmatrix} h_1 & h_2 \\ h_2^* & -h_1^* \end{bmatrix} \begin{bmatrix} x_1 \\ x_2 \end{bmatrix} +\begin{bmatrix} h_1 & h_2 \\ h_2^* & -h_1^* \end{bmatrix}\begin{bmatrix} n_1 \\ n_2^* \end{bmatrix} \\ = \frac{1}{||h_1||^2+||h_2||^2}\begin{bmatrix} x_1 \\ x_2 \end{bmatrix}+\begin{bmatrix} h_1 & h_2 \\ h_2^* & -h_1^* \end{bmatrix}\begin{bmatrix} n_1 \\ n_2^* \end{bmatrix} \end{align}\]

Signal vector $x$에 곱해진 $\frac{1}{

h_1

^2+

h_2

^2}$는 상수이므로 신호의 정보를 훼손하지 않는다.

Rayleigh fading

좀 더 상세한 논의를 위해 Rayleigh fading을 살펴본다.

\[\begin{align} h=h_r+jh_i \\ h_r, h_i\sim\mathcal{N}(0,\frac{1}{\sqrt{2}}^2) \end{align}\]

Rayleigh fading은 위와 같이 실수부, 허수부로 분리되며, Rayleigh distribution을 따른다.

Channel vector $h$는 Rayleigh distribution 특성 따라 다음이 성립한다.

\[\begin{align} &E[|h|] = \frac{\sqrt\pi}{2} \\ &Var[|h|]=1-\frac{\pi}{4} \\ &Var[|h|]=E[|h|^2]-E[|h|]^2 \\ &1-\frac{\pi}{4}=E[|h|^2]-\frac{\pi}{4} \\ &E[|h|^2]=1 \end{align}\]

Channel gain의 각 요소의 평균 크기가 1이라는 점을 주목하며 Decoding된 신호 \(\frac{1}{||h_1||^2+||h_2||^2}\begin{bmatrix} x_1 \\ x_2 \end{bmatrix}\) 를 다시 생각해보자. $\frac{1}{||h_1||^2+||h_2||^2}$는 평균적으로 $\frac{1}{2}$이 되므로 Signal vector의 power를 절반 감소시킨다. 하지만 channel matrix가 AWGN에 곱해지며 noise power도 감소시키는 효과 또한 발생한다.